BFS
1) BFS란?
Breadth-First Search (너비 우선 탐색)의 약어로
그래프 또는 트리 구조에서 루트(시작점)에서부터 가까운 노드부터 차례대로 탐색해 나가는 알고리즘입니다.
탐색 대상의 깊이보다는 너비(수평)를 먼저 탐색한다는 특징이 있습니다.
즉, 시작 노드에 연결된 모든 이웃 노드를 먼저 방문하고, 그 다음에는 그 이웃들의 이웃 노드를 탐색하는 방식입니다.
BFS는 보통 큐(Queue) 자료구조를 사용하여 구현됩니다.
2) BFS 시간복잡도
| 요소 | 설명 |
| 시간 복잡도 | O(V + E) → V: 정점 수, E: 간선 수 |
| 공간 복잡도 | O(V) → 큐와 방문 리스트 저장 용도 |
BFS는 모든 정점을 한 번씩 방문하고, 각 간선도 한 번씩 확인하기 때문에, 총 연산량은 노드 수 + 간선 수에 비례합니다.
3) BFS 활용분야
| 분야 | 설명 |
| 경로 탐색 | 최단 경로 탐색 (ex. 미로 탈출, 지하철 길찾기) |
| 소셜 네트워크 분석 | 친구 추천 (n단계 친구 탐색) |
| AI 탐색 알고리즘 | 퍼즐 문제, 게임 맵 탐색 |
| 네트워크 | 최소 홉 수 계산 (라우팅, 브로드캐스팅 등) |
| 웹 크롤링 | 링크 따라가며 층별로 탐색 |
4) BFS 동작원리
1. 시작 노드를 큐에 넣고, 방문 표시
2. 큐에서 노드를 꺼내 인접 노드를 확인
3. 아직 방문하지 않은 인접 노드를 큐에 추가하고 방문 표시
4. 큐가 빌 때까지 2~3번 반복
5) 예시를 통한 동작원리 설명

이 예시를 통해 어떤 단계로 BFS가 진행되는지 확인해보자.
STEP 0: 시작 노드 A 방문
동작: 시작 노드 A를 방문하고, 인접 노드인 B, C를 큐에 삽입
큐 결과: ['B', 'C']
✅ 방문: A
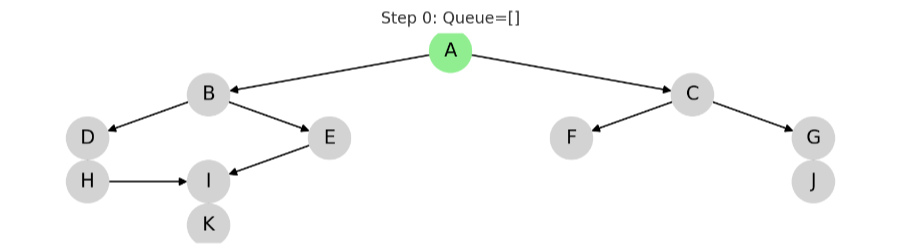
STEP 1: B 방문
동작: B를 큐에서 꺼내고, 인접 노드 D, E를 큐에 추가
큐 결과: ['C', 'D', 'E']
✅ 방문: A, B
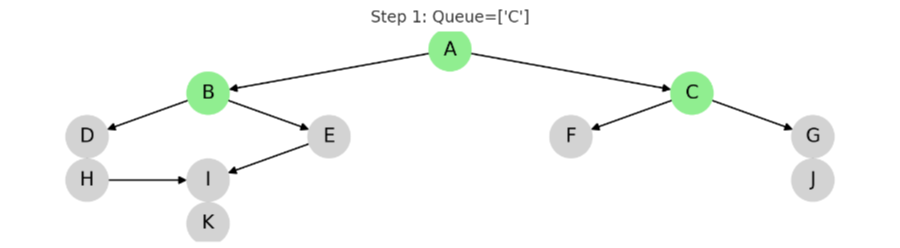
STEP 2: C 방문
동작: C를 큐에서 꺼내고, 인접 노드 F, G를 큐에 추가
큐 결과: ['D', 'E', 'F', 'G']
✅ 방문: A, B, C
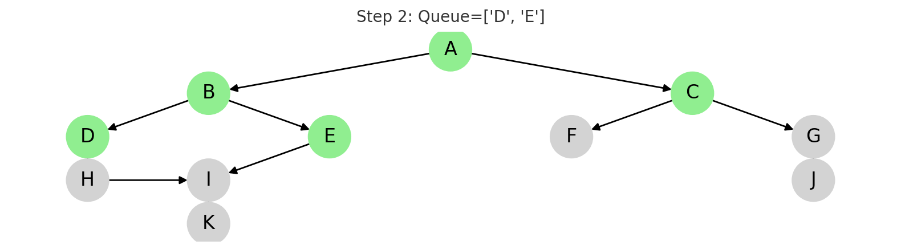
STEP 3: D 방문
동작: D를 큐에서 꺼내고, 자식 노드 H를 큐에 추가
큐 결과: ['E', 'F', 'G', 'H']
✅ 방문: A, B, C, D
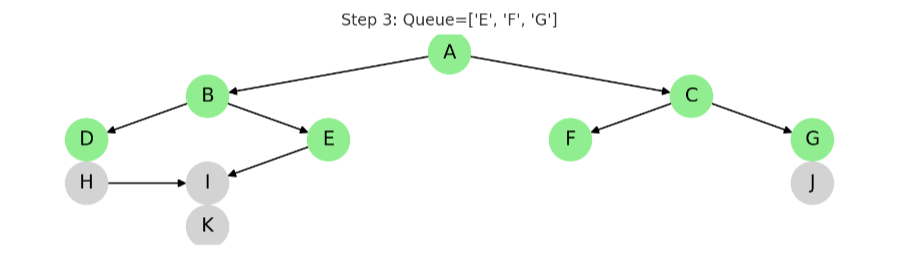
STEP 4: E 방문
동작: E를 큐에서 꺼내고, 자식 노드 I를 큐에 추가
큐 결과: ['F', 'G', 'H', 'I']
✅ 방문: A, B, C, D, E
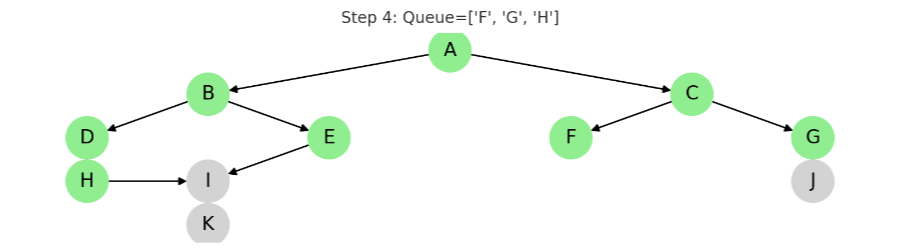
STEP 5: F 방문
동작: F는 자식 노드가 없어 큐에서 제거만 수행
큐 결과: ['G', 'H', 'I']
✅ 방문: A, B, C, D, E, F
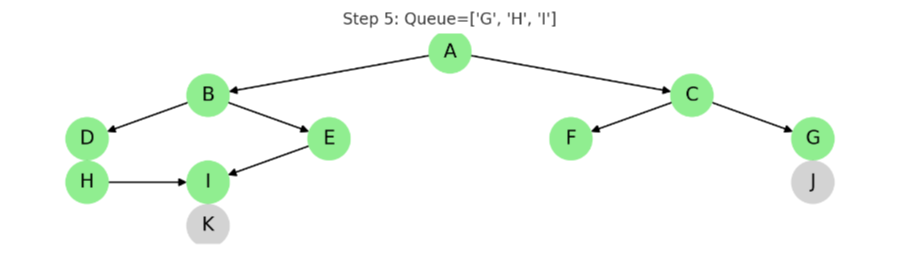
STEP 6: G 방문
동작: G를 큐에서 꺼내고, 자식 노드 J를 큐에 추가
큐 결과: ['H', 'I', 'J']
✅ 방문: A, B, C, D, E, F, G
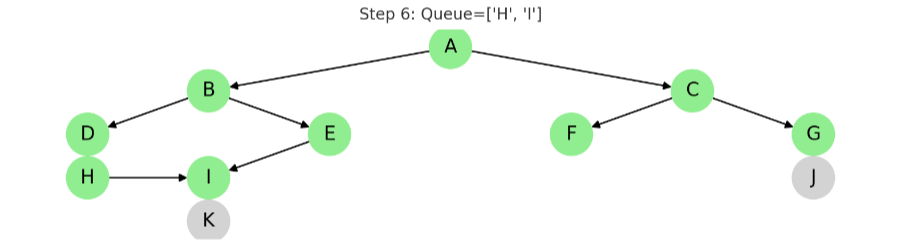
STEP 7: H 방문
동작: H를 큐에서 꺼내고, 자식 노드 I가 이미 방문된 상태라 무시
큐 결과: ['I', 'J']
✅ 방문: A, B, C, D, E, F, G, H
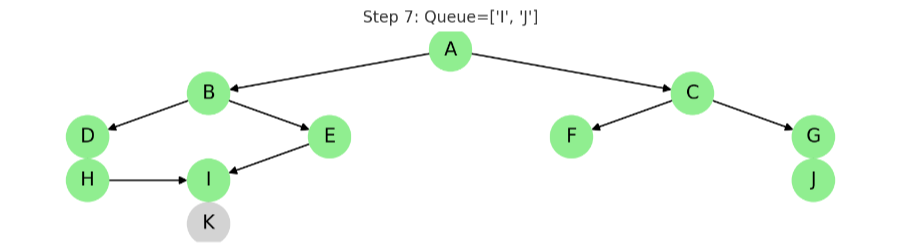
STEP 8: I 방문
동작: I를 큐에서 꺼내고, 자식 노드 K를 큐에 추가
큐 결과: ['J', 'K']
✅ 방문: A, B, C, D, E, F, G, H, I
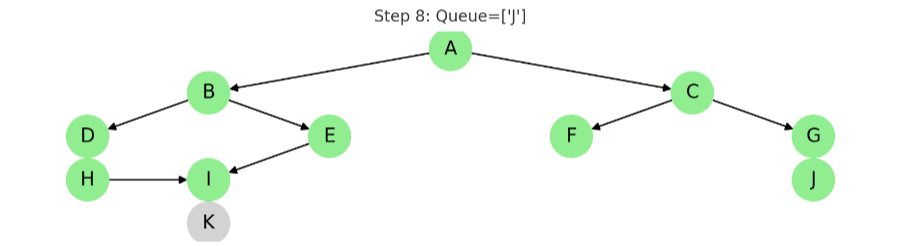
STEP 9: J 방문
동작: J는 자식 노드 없음
큐 결과: ['K']
✅ 방문: A, B, C, D, E, F, G, H, I, J
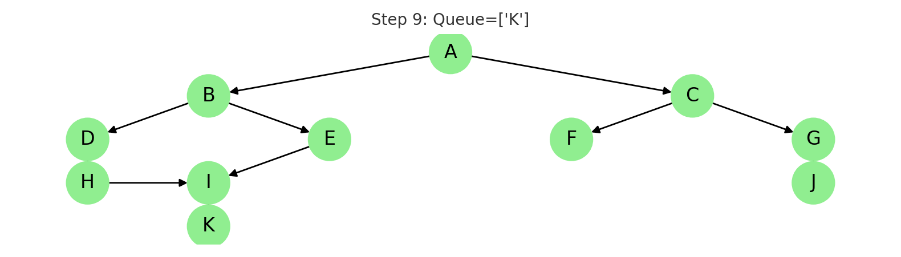
STEP 10: K 방문
동작: K를 큐에서 꺼냄. 더 이상 인접 노드 없음
✅ 방문: A, B, C, D, E, F, G, H, I, J, K

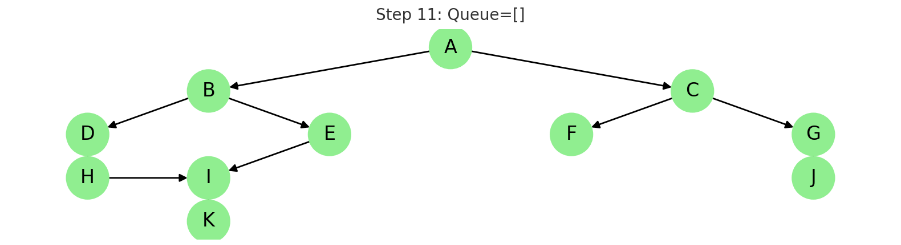
STEP 11: 종료
동작: BFS 종료
모든 노드를 한 번씩 방문 완료
6) Java로 구현한 BFS 예제 코드
import java.util.*;
public class BFSExample {
// 그래프를 인접 리스트 형태로 표현
private Map<String, List<String>> graph = new HashMap<>();
// 노드와 간선을 추가하는 함수
public void addEdge(String node, String neighbor) {
graph.computeIfAbsent(node, k -> new ArrayList<>()).add(neighbor);
}
// BFS 탐색 함수
public void bfs(String start) {
Set<String> visited = new HashSet<>();
Queue<String> queue = new LinkedList<>();
// 시작 노드 처리
queue.offer(start);
visited.add(start);
while (!queue.isEmpty()) {
String current = queue.poll();
System.out.print(current + " ");
// 인접 노드 순회
List<String> neighbors = graph.getOrDefault(current, new ArrayList<>());
for (String neighbor : neighbors) {
if (!visited.contains(neighbor)) {
visited.add(neighbor);
queue.offer(neighbor);
}
}
}
}
// 테스트 메인 함수
public static void main(String[] args) {
BFSExample bfs = new BFSExample();
// 예제 그래프 구성
bfs.addEdge("A", "B");
bfs.addEdge("A", "C");
bfs.addEdge("B", "D");
bfs.addEdge("B", "E");
bfs.addEdge("C", "F");
bfs.addEdge("C", "G");
bfs.addEdge("D", "H");
bfs.addEdge("E", "I");
bfs.addEdge("H", "I");
bfs.addEdge("I", "K");
bfs.addEdge("G", "J");
System.out.println("BFS 탐색 결과:");
bfs.bfs("A"); // 시작 노드 A
}
}
연관된 문제
https://devwarriorjungi.tistory.com/entry/%EB%B0%B1%EC%A4%80-1926-Java-%EA%B7%B8%EB%A6%BC
[백준 1926] Java - 그림
그림 https://www.acmicpc.net/problem/1926 1) 문제어떤 큰 도화지에 그림이 그려져 있을 때, 그 그림의 개수와 가장 넓은 그림의 넓이를 출력하여라.그림은 1로 연결된 영역이고, 가로나 세로로만 연결된
devwarriorjungi.tistory.com
'Algorithm > 이론' 카테고리의 다른 글
| 재귀함수 (Recursion) (0) | 2025.05.02 |
|---|---|
| DFS 깊이 우선 탐색 (스택 방식) (0) | 2025.05.01 |
| DFS 깊이 우선 탐색 (재귀방식) (0) | 2025.05.01 |
| 복잡도 (0) | 2025.05.01 |
